1 - 0,999... = 0 ?

[Verhulst]

Ich möchte noch mal auf das Kernproblem aufmerksam machen, aus welchem sich alle diese Randprobleme 1=0,999 und andere (lim 1/n = 0 mit n€N)
ergeben.
Das Kernproblem (aus der Urteilchentheorie) lautet:

Ist die Vereinigung von abzählbar vielen abzählbaren Mengen abzählbar oder unendlich.

1.
Eine Menge ist abzählbar, lassen sich ihre Elemente (der Größe nach) ordnen (Menge der natürlichen Zahlen 1,2,3,...)
2.
Eine Menge heißt überabzählbar (oder unendlich), ist eine solche Ordnung nicht möglich, wie das bei der Menge der reellen Zahlen der Fall ist. Wir kennen den Nachfolger von Null und 1 und 2 und PI und ... nicht und können deshalb alle diese (reellen) Zahlen nicht (der Größe nach) ordnen.

Konkret:
Wir ersetzen in der Menge der natürlichen Zahlen N = {1,2,3....}
jede Zahl durch die Menge N selbst und erhalten so eine Menge, welche eine Vereinigung von abzähbar vielen (1,2,3,...) Mengen ist, von der jede abzählbar ist.
Wir bilden also, unmathematisch formuliert N+N+N+N... (ohne Ende)
Ist nun diese Menge abzählbar oder nicht?
Können wir alle Elemente durchzählen oder nicht, haben wir abzählbar viele Einsen und Zweien und... vorliegen?
Ist die Menge abzählbar oder überabzählbar. Darum geht es im Kern.
CANTOR (und mit ihm die Mathematik) sagt, sie sei abzählbar. Ich sage: Sie ist überabzählbar.

Selbstverständlich ist diese Menge abzählbar; darauf beruht doch die Def. für Abzählbarkeit. Deine Menge enthält übrigens wiederum nur die Natürlichen Zahlen, bei der eben die geforderte Ordnung möglich ist. Hieraus kannst Du also keine überabzählbare Menge konstruieren.

[Elrik]

Ich möchte noch mal auf das Kernproblem aufmerksam machen, aus welchem sich alle diese Randprobleme 1=0,999 und andere (lim 1/n = 0 mit n€N)
ergeben.
Das Kernproblem (aus der Urteilchentheorie) lautet:

Ist die Vereinigung von abzählbar vielen abzählbaren Mengen abzählbar oder unendlich.

1.
Eine Menge ist abzählbar, lassen sich ihre Elemente (der Größe nach) ordnen (Menge der natürlichen Zahlen 1,2,3,...)
2.
Eine Menge heißt überabzählbar (oder unendlich), ist eine solche Ordnung nicht möglich, wie das bei der Menge der reellen Zahlen der Fall ist. Wir kennen den Nachfolger von Null und 1 und 2 und PI und ... nicht und können deshalb alle diese (reellen) Zahlen nicht (der Größe nach) ordnen.

Konkret:
Wir ersetzen in der Menge der natürlichen Zahlen N = {1,2,3....}
jede Zahl durch die Menge N selbst und erhalten so eine Menge, welche eine Vereinigung von abzähbar vielen (1,2,3,...) Mengen ist, von der jede abzählbar ist.
Wir bilden also, unmathematisch formuliert N+N+N+N... (ohne Ende)
Ist nun diese Menge abzählbar oder nicht?
Können wir alle Elemente durchzählen oder nicht, haben wir abzählbar viele Einsen und Zweien und... vorliegen?
Ist die Menge abzählbar oder überabzählbar. Darum geht es im Kern.
CANTOR (und mit ihm die Mathematik) sagt, sie sei abzählbar. Ich sage: Sie ist überabzählbar.

Was wenn beides keinen Sinn ergibt, diese Menge also weder abzählbar noch überabzählbar ist? N ist eine mit Zählen und durch eine Zahl bestimmte Menge und damit nicht nur bereits gezähltes Element von n sondern stärkste und schwächste, kurz einzige Eigenschaft von n, der Menge aller natürlichen Zahlen. Warum soll man Elemente einer Menge zählen, die bei näherer Betrachtung keine Elemente, sondern Zeichen, nämlich Ziffern sind, wie Einsen, Zweien, Dreien usw.?

[Verhulst]

Was wenn beides keinen Sinn ergibt, diese Menge also weder abzählbar noch überabzählbar ist? N ist eine mit Zählen und durch eine Zahl bestimmte Menge und damit nicht nur bereits gezähltes Element von n sondern stärkste und schwächste, kurz einzige Eigenschaft von n, der Menge aller natürlichen Zahlen. Warum soll man Elemente einer Menge zählen, die bei näherer Betrachtung keine Elemente, sondern Zeichen, nämlich Ziffern sind, wie Einsen, Zweien, Dreien usw.?

Nun kann eine Menge, so sie etwas enthält, nur Elemente enthalten; Du darfst diese Elemente gerne Zeichen, Ziffern oder Elriks nennen ...

Das, was Todoroff formuliert hat, kann am anschaulichsten als kartesisches Koordinatensystem dargestellt werden; wir brauchen im zu betrachtenden Fall nur den ersten Quadranten. So werden etwa in der Abszisse die Natürlichen Zahlen dargestellt. Über jeden Punkt entlang der Abszisse stehen als Mengen wiederum jeweils die Natürlichen Zahlen, diesmal parallel zur Ordinate - dieses nun wäre das, was Todoroff mit "Wir bilden also, unmathematisch formuliert N+N+N+N... (ohne Ende)" meint. Da sich nun eindeutig jeweils Koordinaten zu diesen Punkten bestimmen, d. h. zuordnen lassen, ist damit der Beweis der Abzählbarkeit erbracht.


zur

[Elrik]

Was wenn beides keinen Sinn ergibt, diese Menge also weder abzählbar noch überabzählbar ist? N ist eine mit Zählen und durch eine Zahl bestimmte Menge und damit nicht nur bereits gezähltes Element von n sondern stärkste und schwächste, kurz einzige Eigenschaft von n, der Menge aller natürlichen Zahlen. Warum soll man Elemente einer Menge zählen, die bei näherer Betrachtung keine Elemente, sondern Zeichen, nämlich Ziffern sind, wie Einsen, Zweien, Dreien usw.?

Nun kann eine Menge, so sie etwas enthält, nur Elemente enthalten; Du darfst diese Elemente gerne Zeichen, Ziffern oder Elriks nennen ...

Das, was Todoroff formuliert hat, kann am anschaulichsten als kartesisches Koordinatensystem dargestellt werden; wir brauchen im zu betrachtenden Fall nur den ersten Quadranten. So werden etwa in der Abszisse die Natürlichen Zahlen dargestellt. Über jeden Punkt entlang der Abszisse stehen als Mengen wiederum jeweils die Natürlichen Zahlen, diesmal parallel zur Ordinate - dieses nun wäre das, was Todoroff mit "Wir bilden also, unmathematisch formuliert N+N+N+N... (ohne Ende)" meint. Da sich nun eindeutig jeweils Koordinaten zu diesen Punkten bestimmen, d. h. zuordnen lassen, ist damit der Beweis der Abzählbarkeit erbracht.


zur

Nur dass es sich dabei nicht länger um Elemente der natürlichen Menge handelt. Denn wie gesagt beginnt man dank Urteilchen bei eins zu zählen. Eins ist somit und soweit kleinstes und größtes, kurz "einziges" Element der natürlichen Menge. Die natürliche Menge ist die Zahl ihrer Elemente, sind alle gezählten natürlichen Elemente. Die Menge ist nicht abzählbar, Elemente sind abzählbar sind überabzählbar, denn bei tausend Sandkörnern ist noch lang nicht Schluss.

[Todoroff]

Das, was Todoroff formuliert hat, kann am anschaulichsten als kartesisches Koordinatensystem dargestellt werden; wir brauchen im zu betrachtenden Fall nur den ersten Quadranten. So werden etwa in der Abszisse die Natürlichen Zahlen dargestellt. Über jeden Punkt entlang der Abszisse stehen als Mengen wiederum jeweils die Natürlichen Zahlen, diesmal parallel zur Ordinate - dieses nun wäre das, was Todoroff mit "Wir bilden also, unmathematisch formuliert N+N+N+N... (ohne Ende)" meint. Da sich nun eindeutig jeweils Koordinaten zu diesen Punkten bestimmen, d. h. zuordnen lassen, ist damit der Beweis der Abzählbarkeit erbracht.

Nun, wenn es so einfach wäre, wäre es kein Problem. Es ist aber eines.

[Verhulst]

Das, was Todoroff formuliert hat, kann am anschaulichsten als kartesisches Koordinatensystem dargestellt werden; wir brauchen im zu betrachtenden Fall nur den ersten Quadranten. So werden etwa in der Abszisse die Natürlichen Zahlen dargestellt. Über jeden Punkt entlang der Abszisse stehen als Mengen wiederum jeweils die Natürlichen Zahlen, diesmal parallel zur Ordinate - dieses nun wäre das, was Todoroff mit "Wir bilden also, unmathematisch formuliert N+N+N+N... (ohne Ende)" meint. Da sich nun eindeutig jeweils Koordinaten zu diesen Punkten bestimmen, d. h. zuordnen lassen, ist damit der Beweis der Abzählbarkeit erbracht.

Nun, wenn es so einfach wäre, wäre es kein Problem. Es ist aber eines.

Und? Brauchst Du noch arg lange, bis Dir eine Begründung einfällt? ;-)




Sapere aude!

Verhulst

[Elrik]

Es gab mal jemanden der eine runde Torte die sechs centimeter hoch war in drei gleichgroße Teile schneiden sollte. Er nahm dazu drei Fäden die länger waren als der Durchmesser der Torte spannte sie in zwei centimentern abstand übereinander und schnitt die Torte ind drei Scheiben. Einer bekam nun das Obere stück mit Sahnehäupchen ein anderer bekam nun das mittlere stück und ein anderer den Boden. Ist das nicht ein geniales Realitätsbewußtsein?

[LaughingMan]

Hallo allerseits!

Erörtern Sie mal, wie denn ein endlicher Wert (1/9) einem endlosen Wert (0,111...) überhaupt gleich sein kann?

Da fällt mir das Paradoxon von Achilles und der Schildkröte ein. Im Original kommen keine Zahlen vor, aber ich füge mal einige hinzu, um das obige Problem zu illustireren:

Achilles und eine Schildkröte sollen um die Wette laufen. Nun ist Achilles aber 10mal schneller und damit's ein bisschen spannender wird, bekommt die Schildkröte 100 Meter Vorsprung. Auf "Los!" geht's los und beide legen sich ins Zeug.
Nach einer gewissen Zeit hat Achilles die 100 Meter zurück gelegt, aber die Schildkröte ist mittlerweile ja ein Zehntel dessen gelaufen und befindet sich weitere 10 Meter von der Startlinie entfernt (mittlerweile also 110 Meter = 0,11 Kilometer). Kurze Zeit darauf ist Achilles bei Meter 110 angekommen, aber die Schildkröte hat er immernoch nicht eingeholt, denn die ist mittlerweile bei 111 Meter. Ist er dort angekommen beträgt sein Rückstand immerhon noch 10 cm (die Schildkröte ist bei Kilometer 0,1111) usw. Dies ist ein endloser Prozess und führt (in Kilometern gemessen) langsam auf die Zahl 0,111... zu.

@Mileva: Also kann Achilles die Schildkröte nie überholen, weil es ein endloser Prozess ist? Oder kann eine endlose Summe doch einen endlichen Wert haben?

Entweder ist etwas definitiv endlich oder eben nicht.

Richtig! Die Darstellung von 1/9 im Dezimalsystem ist unendlich lang und nicht endlich lang - der Wert von 1/9 ist in allen Darstellungen endlich groß und nicht unendlich groß.

Außerdem wunder ich mich, warum man sich ständig auf das Dezimalsystem festlegt. Wählt man statt 10 z.B. 3 als Basis kann man 1/9 als 0,01 darstellen. Andersherum wird's dann aber z.B. mit 1/10 schwierig.

[Elrik]

Also kann Achilles die Schildkröte nie überholen, weil es ein endloser Prozess ist? Oder kann eine endlose Summe doch einen endlichen Wert haben?

Wichtig ist bei einem Wettlauf nicht, bei wieviel Metern Achilis die Schildkröte überholt, sondern wer als erster am Ziel ist, welches uns vorenthalten wurde, denn wie lang ist die Rennstrecke?

[Todoroff]

LaughingMan
Also kann Achilles die Schildkröte nie überholen, weil es ein endloser Prozess ist?
Wäre es ein endloser Prozess, kämen beide zum Stillstand.

Oder kann eine endlose Summe doch einen endlichen Wert haben?
Eine endlose Summe hat nach gegenwärtiger Mathematik einen endlichen Wert als Ergebnis, was ein Widerspruch in sich ist, den es aufzulösen gilt.
q.e.d.

Was wollen Sie uns mitteilen?

Joh 3,3
Jesus antwortete ihm: Amen, amen, Ich sage dir: Wenn jemand nicht von neuem geboren wird, kann er das Reich Gottes nicht sehen.
http://www.gtodoroff.de/wiegott.htm

[irgendwer]

Herr Todoroff:
ihre Frage: 1- 0.99999.... = 0?
Antwort: JA.

x=0.99999... /multipliziere mit 10
10x= 9.99999.... /subtrahiere x
9x = 9 / dividiere durch 9
x = 1

also ist 1=0.99999.... und damit 1 - 0.99999 = 0.
dann wäre das hoffentlich geklärt.


Abzählbarkeit

Konkret:
Wir ersetzen in der Menge der natürlichen Zahlen N = {1,2,3....}
jede Zahl durch die Menge N selbst und erhalten so eine Menge, welche eine Vereinigung von abzähbar vielen (1,2,3,...) Mengen ist, von der jede abzählbar ist.
Wir bilden also, unmathematisch formuliert N+N+N+N... (ohne Ende)
Ist nun diese Menge abzählbar oder nicht?
Können wir alle Elemente durchzählen oder nicht, haben wir abzählbar viele Einsen und Zweien und... vorliegen?
Ist die Menge abzählbar oder überabzählbar. Darum geht es im Kern.
CANTOR (und mit ihm die Mathematik) sagt, sie sei abzählbar. Ich sage: Sie ist überabzählbar.

Tut mir Leid ihnen mitteilen zu müssen, dass sie falsch sagen und Cantor doch recht hatte.

Eine Menge A ist abzählbar wenn eine Bijektion zwischen A und N (den natuerlichen Zahlen) existiert.
Eine Solche Funktion zu finden ist für ihr Bsp. nicht alzu schwer...
Sei das tupel (j,i), das i-te element aus der j-ten Menge. Diese Tupel können wir ordnen bzw. durchnumerieren, also existiert die Bijektion
z.B. : (1,1), (1,2),(2,1), (1,3),(2,2),(3,1), (1,4),(2,3),(3,2),(4,1), (1,5),(2,4),(3,3),(4,2),(5,1), (1,6)....
Ich hoffe sie erkennen das Muster ;)

(das ist glaub übrigens auch das was Verhulst gemeint hat mit dem koordinaten System)

[Todoroff]

irgendwer
So, so, da haben wir uns wieder einen ganz Schlauen eingefangen.

1- 0.99999.... = 0?
Antwort: JA.
Falsch!

x=0.99999... /multipliziere mit 10
/ multipliziere mit 10
10x= 9.99999.... /subtrahiere x
/ subtrahiere x
9x = 9 / dividiere durch 9
/ dividiere durch 9
x = 1
x=0
also ist 1=0.99999.... und damit 1 - 0.99999 = 0.
dann wäre das hoffentlich geklärt.
das wäre hoffentlich geklärt.
Saubere Mathematik, gelle.


Abzählbarkeit

Konkret:
Wir ersetzen in der Menge der natürlichen Zahlen N = {1,2,3....}
jede Zahl durch die Menge N selbst und erhalten so eine Menge, welche eine Vereinigung von abzähbar vielen (1,2,3,...) Mengen ist, von der jede abzählbar ist.
Wir bilden also, unmathematisch formuliert N+N+N+N... (ohne Ende)
Ist nun diese Menge abzählbar oder nicht?
Können wir alle Elemente durchzählen oder nicht, haben wir abzählbar viele Einsen und Zweien und... vorliegen?
Ist die Menge abzählbar oder überabzählbar. Darum geht es im Kern.
CANTOR (und mit ihm die Mathematik) sagt, sie sei abzählbar. Ich sage: Sie ist überabzählbar.

Tut mir Leid ihnen mitteilen zu müssen, dass sie falsch sagen und Cantor doch recht hatte.
Es tut mir leid, Ihne mitteilen zu müssen, daß Sie irren und ebenso Cantor.

Eine Menge A ist abzählbar wenn eine Bijektion zwischen A und N (den natuerlichen Zahlen) existiert.
Eine Solche Funktion zu finden ist für ihr Bsp. nicht alzu schwer...
Sei das tupel (j,i), das i-te element aus der j-ten Menge. Diese Tupel können wir ordnen bzw. durchnumerieren, also existiert die Bijektion
z.B. : (1,1), (1,2),(2,1), (1,3),(2,2),(3,1), (1,4),(2,3),(3,2),(4,1), (1,5),(2,4),(3,3),(4,2),(5,1), (1,6)....
Ich hoffe sie erkennen das Muster ;)
(das ist glaub übrigens auch das was Verhulst gemeint hat mit dem koordinaten System)
Das habe ich widerlegt. Tut mir schrecklich leid.

Der Tod kann unmöglich Leben gebären.
Also hat es Leben schon vor der
Existenz von Raum und Zeit gegeben.
Georg Todoroff

[LaughingMan]

Ich zitiere mal aus einem anderen Thread:

LaughingMan
Sie leben noch? Von Ihnen haben wir Jahre nichts gelesen.

Ja, ich lebe noch. Freut mich, dass Sie mich wiedererkennen! :-) Ich habe in den letzten Jahren gelegentlich mal reingeschaut und mich nun dazu entschlossen, Mileva die eine oder andere Frage zu stellen. Ich musste allerdings bei jedem meiner Besuche enttäuscht feststellen, dass Sie die Widersprüche ihrer Erweiterungen weiterhin nicht aufgelöst haben. Zur Erinnerung:

Ein widerspruchsfreies System erklären Sie als widersprüchlich[...]

Falls sie die von ihnen nicht gelösten Widersprüche nicht mehr im Kopf haben:

1. Wenn ...999 die größte natürlich Zahl sein soll,warum hat sie dann nicht die Eigenschaften einer natürlichen Zahl (sie hat keinen Nachfolger) ?
Sie wollen die Mathematik erweitern? Gut! Gehen wir die Eigenschaften mal durch: ...999 hat keinen Nachfolger. Die Zahl kann nicht in endlich vielen Schritten aus einer anderen natürlichen Zahl erzeugt werden und es gelten keine Verknüpfungen auf ihr. Alle diese Eigenschaften hat unendlich auch. Sie erweitern also um . Gut gemacht...

2. Zur Vereinfachung: . Sie behaupteten mal Folgendes (kann ich leider nicht mehr nachweisen):
(1)
Außerdem gilt (2) auch für , denn das soll ja in liegen.
Es lässt sich also leicht schlussfolgern: , also .

3. Wenn gilt, warum dann nicht Und wenn doch: ist nicht die kleinste Zahl größer Null?

[...]

[...] und mehrere sich hoffnungslos widersprechende Systeme (RTh, UTh, ETh) als wahr, als widerspruchsfrei.

Erklärte ich wo genau?

Aber andere haben sich ja zumindest an Punkt 1 versucht.

Denken Sie sich ein Koordinatensystem, welches ausschließlich natürliche Zahlen aufweist. Läge prinzipiell in endloser Ferne die Zahl ...999,0 auf der positiven x-Achse, ja oder nein? Falls ja, so ist diese auch als eine natürliche Zahl zu bewerten, warum auch nicht? Theoretisch könnte man durchaus bis zu dieser Zahl unter alleiniger Anwendung natürlicher Zahlen zählen, womit diese eine natürliche Zahl ist. Sind Sie fortwährend anderer Ansicht, begründen Sie diese, bitte!

Als Antwort auf die Frage mit dem Koordinatensystem: Aus 1. (s.u.) folgt ganz klar "Nein". Aber du meinst ja auch nicht die natürlichen Zahlen, sondern eure Erweiterung. Diese folgt (s.u. 2.) bisher aber keinen Regeln, also kann ich die Frage nicht beantworten.

Ich versuch's mal zweigleisig:

1. Aus Sicht der herrschenden Mathematik ist die Erklärung, warum ...999,0 keine natürliche Zahl ist, sehr einfach: sie hat keinen Nachfolger, also erfüllt sie nicht die Peano-Axiome. Diese sind (bei Wikipedia entliehen und leicht verändert):
   1. 1 ist eine natürliche Zahl.
   2. Zu jeder natürlichen Zahl n gibt es genau einen Nachfolger n', der ebenfalls eine natürliche Zahl ist.
   3. Es gibt keine natürliche Zahl, deren Nachfolger 1 ist.
   4. Jede natürliche Zahl ist Nachfolger höchstens einer natürlichen Zahl.
   5. Von allen Mengen X, welche
      • die Zahl 1 und
      • mit jeder natürlichen Zahl n auch stets deren Nachfolger n'
      enthalten, ist die Menge der natürlichen Zahlen die kleinste.
   Eine Menge, die das nachfolgerlose Element ...999,0 enthält, ist also nicht isomorph zu (vulga: "gleich") den natürlichen Zahlen. Eigentlich ist die Sache damit gelaufen, denn die natürlichen Zahlen sind per definitionem jene, welche durch die Peano-Axiome entstehen.
2. Nun versuche ich es mal aus deiner Sicht. Wenn ...999,0 aber unbedingt zu den natuerlichen Zahlen gehören soll, muss dazu ein passendes Axiomensystem angegeben werden! Ohne handelt es sich einfach um eine willkürliche Menge, die keine interessanten beweisebaren Eigenschaften hat.
   Was ich mich auch frage: Normalerweise stören dich nicht-endende Prozesse doch immer - warum gerade bei ...999,0 die Ausnahme? Wenn man theoretisch unter alleiniger Anwendung natürlicher Zahlen bis zu dieser Zahl zählen kann, so gib die Rechenvorschrift bitte an! Und wenn dieser Prozess ...999,0 ergibt, warum ergibt eine Addition mit Eins dann nicht 10...0,0>...999,0. Natürlich kann man die endlose (ist das hier der richtige Begriff?) Folge von Nullen nicht aufschreiben, aber das geht mit den Neunen ja auch nicht und scheint kein Problem darzustellen.

Da ich glaube, dass die Einführung eines Axiomensystem für eure natuerlichen Zahlen unbedingten Vorrang hat, bitte ich dich darum, dich dem zuerst zuzuwenden - der Vollständigkeit halber gehe ich hier aber auch auf deine Aussagen zum Thema Unendlich ein:

Unendlich ist im Gegensatz zu ...999,0 keine Zahl, sondern ein Begriff, nicht mehr. Schon darin unterscheidet sich Unendlich von der denkbar größten natürlichen Zahl. Wichtiger ist aber der Unterschied, dass Unendlich reichlich mehr umfasst als ...999,0, die ja ausschließlich natürliche Zahlen "enthält", während Unendlich auch alle rationalen und irrationalen Zahlen miteinbezieht. Unendlich muss also weitaus mehr sein als ...999,0 und damit nicht identisch mit letzterer Zahl. Was ist daran so schwer?

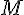
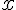
Du machst es schwer, indem du das Wort Unendlich im sprachlich gebräuchlichen Sinne verwendest und diese Eigenschaften auf das mathematische Konstrukt zu übertragen versuchst. Im mathematischen Sinne "enthält" gar nichts (sonst wäre es ja eine Menge), sondern ist zu einer gegebenen Menge und einer auf ihr definierten Ordnung (also z.B. mit dem üblichen "kleiner/gleich") einfach das Element für welches gilt: .
Nun kann wegen der üblichen Rechenregeln (Addition um 1 führt zu einem größeren Element) für oder oder oder aber nicht gelten (streng genommen ist dann auch der obige Vergleich nicht definiert, aber das Problem lässt sich ausräumen).

1 dividiert durch Unendlich ergibt Null - auch laut herrschender Mathematik.

Nein, nein, nein! In der herrschenden Mathematik ist kein Element der natürlichen, ganzen, rationalen oder reellen Zahlen und es gibt - allein schon deswegen - keinerlei definierte Rechenoperationen mit diesem Element!
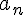
Es mag sein, dass mal jemand schlampig oder ähnliches aufschreibt, aber das ist immer nur eine unsaubere Abkürzung für wobei eine unbeschränkte Folge ist! (Die Definition dieses Grenzwertbegriffes gibt's hier im Forum mehrfach und auch da taucht das Konzept der Unendlichkeit in keiner Form auf - das unter dem Limes ist einfach nur Notation.)

Bitte achte also darauf, den Begriff "Unendlich" im Zusammenhang mit der herrschenden Mathematik nicht durch sprachliche Semantik zu überladen, sondern in dem simplen Sinne zu verwenden, der definiert ist. Falls du neue Unendlichkeitskonzepte einführen möchtest (so wohl "endlos" und "unendlich") definiere diese bitte ordentlich.

Unendlich ist das Überabzählbare, endlos das Abzählbare.

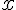
Das ist keine Definition, denn "das Abzählbare" und "das Überabzählbare" sind in der Mathematik bisher keine Begriffe. Es gibt wohl abzählbare und überabzählbare Mengen, aber keine Verallgemeinung dieser Begriffe. Auch haben diese Unendlichkeitsbegriffe nichts mit dem zu tun, das größer als alle Elemente einer Menge ist. Es handelt sich um unterschiedliche Definitionen in unterschiedlichen Teilgebieten, die nur einige sprachliche Gemeinsamkeiten haben.

Ganz gut zum Einlesen ist dieser Wikipedia-Artikel geeignet.



PS: Du kannst mich gerne Duzen oder auch darauf bestehen, dass ich Sieze.

[irgendwer]

Herr Todoroff:

ist nicht definiert!!!!!! Können sie auf Wikipedia und verschiedenen Büchern zu Analysis I lesen.

ist schwachsinn. bzw. es ist genau so wahr wie: ; oder auch: ...
In meiner Rechnung, habe ich keine Operation benutzt die nicht definiert ist, oder ähnliches. Sie hingegen schon nämlich eben , und sie definieren es in diesem Zusammenhang selber nach Lust und Laune, um das zu zeigen, was sie zeigen wollen.


Zur abzählbarkeit:
Sie behaupten das widerlegt zu haben, sagen aber nicht wie.
abgesehen davon:
Ich habe ihnen ein Bsp. für eine Bijektive Abbildung , gezeigt.

Also bitte nicht einfach ins leere behaupten sondern zeigen....

[Todoroff]

irgendwer
Die Beweise befinden sich alle auf meiner HP und in meinen Büchern. Ich gedenke nicht, mich hier zu wiederholen.

Jer 21,8
Zu diesem Volk aber sollst du sagen: So spricht der Herr: Seht den Weg des Lebens und den Weg des Todes stelle ich euch zur Wahl.